We will have situation as shown in figure in attachment.
Here OH is the hill of height 21 feet.
Statute is HS, so lets its height be h, so HS = h
Distance OA = 57 feet, observer distance from base of hill
Then ∠HAS = 7.1° (angle subtended by statue HS at point A)
First we wil find ∠OAH in right ΔOAH
so let ∠OAH be Ф
We will use
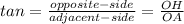
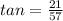
so
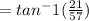
Ф = 20.22°
Now in right ΔOAS, we have
∠OAS = Ф + 7.1° = 20.22° +7.1° = 27.32°
so tan (27.32°) =
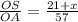
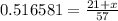
Now we will solve for x here
So multiply both sides by 57
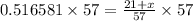
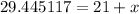
29.445117 -21 =21 + x -21
8.445 = x
So height of statue is 8.45 feet.