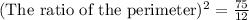Answer:
The ratio of their perimeter is 5 : 2.
Explanation:
Since, if two triangles are similar,
Then, the ratio of their area is equal to the square of the ratio of corresponding sides or the ratio of the corresponding perimeters,
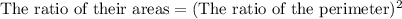
Here, the triangles have have areas of 75 m² and 12 m²,
So, the ratio of the area =