For the given function
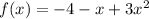 -----------------------(1)
-----------------------(1)
we have to see when it will increase and decrease.
For that we will first find derivative of function
Now derivative of first term in f(x) which is -4 will be 0 as its constant.
then derivative of x is 1, so derivative of -x will be -1
To derivate last term of function,
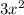 , we will use power rule formula:
, we will use power rule formula:
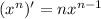
so
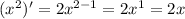
constant 3 will come as it is, so derivative of 3x^2 wil be 3(2x)= 6x.
So f'(x) = 0 -1 +6x
f'(x) = -1 + 6x------------------------------(2)
For function to be increasing f'(x) should be positive and for function to be decreasing f'(x) shoould be negative
So we will first find where f'(x) = 0
So put 0 in f'(x) place in equation (2)
0 = -1 + 6x
Now solve for x as shown
0 +1 = -1 + 6x +1
1 = 6x
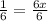
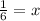
So now we can have two regions as shown on either side of 1/6 on number line
_____________I______________
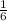 _______II__________
_______II__________
So to test region I, pick any number to the left side of
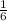 . For example lets take 0. now plug 0 inx place in f'(x) equation given by (2)
. For example lets take 0. now plug 0 inx place in f'(x) equation given by (2)
f'(x)= -1 + 6x
f'(0) = -1 + 6(0) = -1+0 = -1 which is negative. So since f'(x) we got as negative for region I, so this will be decreasing.
Interval for region I will be (-∞,
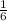 )
)
----------------------------------------------------------------------------------------------------------
similarly now test region II. For that pick any number to the right of
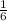 , lets take 1. So plug 1 in x place in f'(x) equation given by (2)
, lets take 1. So plug 1 in x place in f'(x) equation given by (2)
f'(x) = -1 + 6x
f'(1) = -1 +6(1)= -1+6 = 5 which is positive so we will have f(x) increasing in this region.
Interval for region II will be (
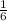 , ∞)
, ∞)
------------------------------------------------------------------------
Graphs of
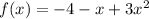 and
and
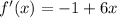 are shown in attachment. So you can clearly see in graph that f'(x) is negative (below x axis) from -∞ till
are shown in attachment. So you can clearly see in graph that f'(x) is negative (below x axis) from -∞ till
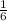 so f(x) should be decreasing in this part which we can see from f(x) graph that its decreasing from -∞ till
so f(x) should be decreasing in this part which we can see from f(x) graph that its decreasing from -∞ till
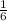 .
.
Similarly f'(x) is positive( above x axis) beyond
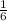 so its increasing beyond
so its increasing beyond
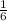 which we can veryify from f(x) graph we can see that its increasing from
which we can veryify from f(x) graph we can see that its increasing from
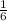 till ∞. Hence verified
till ∞. Hence verified