Question

Find the intervals on which f is increasing and decreasing. Superimpose the graphs of f and f prime to verify your work.

f(x)= -4 - x + 3x^2

Answer 1

For the given function

`f(x) = -4 -x + 3x^2`-----------------------(1)

we have to see when it will increase and decrease.

For that we will first find derivative of function

Now derivative of first term in f(x) which is -4 will be 0 as its constant.

then derivative of x is 1, so derivative of -x will be -1

To derivate last term of function,
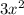`3x^(2)`, we will use power rule formula:

`(x^(n) )'= nx^(n-1)`

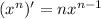
so
`(x^(2) )'= 2x^(2-1) = 2x^(1) = 2x`

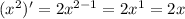
constant 3 will come as it is, so derivative of 3x^2 wil be 3(2x)= 6x.

So f'(x) = 0 -1 +6x

f'(x) = -1 + 6x------------------------------(2)

For function to be increasing f'(x) should be positive and for function to be decreasing f'(x) shoould be negative

So we will first find where f'(x) = 0

So put 0 in f'(x) place in equation (2)

0 = -1 + 6x

Now solve for x as shown

0 +1 = -1 + 6x +1

1 = 6x

`(1)/(6) = (6x)/(6)`

`(1)/(6) = x`

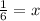
So now we can have two regions as shown on either side of 1/6 on number line

_____________I______________
`(1)/(6)`_______II__________

So to test region I, pick any number to the left side of
`(1)/(6)`. For example lets take 0. now plug 0 inx place in f'(x) equation given by (2)

f'(x)= -1 + 6x

f'(0) = -1 + 6(0) = -1+0 = -1 which is negative. So since f'(x) we got as negative for region I, so this will be decreasing.

Interval for region I will be (-∞,
`(1)/(6)`)

----------------------------------------------------------------------------------------------------------

similarly now test region II. For that pick any number to the right of
`(1)/(6)`, lets take 1. So plug 1 in x place in f'(x) equation given by (2)

f'(x) = -1 + 6x

f'(1) = -1 +6(1)= -1+6 = 5 which is positive so we will have f(x) increasing in this region.

Interval for region II will be (
`(1)/(6)`, ∞)

------------------------------------------------------------------------

Graphs of
`f(x) = -4 -x + 3x^2` and
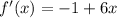`f'(x) = -1 +6x`are shown in attachment. So you can clearly see in graph that f'(x) is negative (below x axis) from -∞ till
`(1)/(6)` so f(x) should be decreasing in this part which we can see from f(x) graph that its decreasing from -∞ till
`(1)/(6)`.

Similarly f'(x) is positive( above x axis) beyond
`(1)/(6)` so its increasing beyond
`(1)/(6)` which we can veryify from f(x) graph we can see that its increasing from
`(1)/(6)` till ∞. Hence verified