Answer:
The variable is 8/7.
Explanation:
Givens

To solve this problem, we need to use the Inscribed Angle Theorem which states that an angle inscribed in a circle is half of the subtended arc.
Based on this theorem, we have
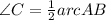
Replacing each expression
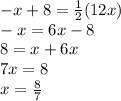
Therefore, the variable is 8/7.