For a better understanding of the solution provided here please find the diagram attached.
Please note that in coordinate geometry, the coordinates of the midpoint of a line segment is always the average of the coordinates of the endpoints of that line segment.
Thus, if, for example, the end coordinates of a line segment are
 and
and
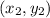 then the coordinates of the midpoint of this line segment will be the average of the coordinates of the two endpoints and thus, it will be:
then the coordinates of the midpoint of this line segment will be the average of the coordinates of the two endpoints and thus, it will be:
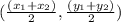
Thus for our question the endpoints are
 and
and
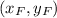 and hence the midpoint will be:
and hence the midpoint will be:
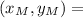
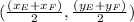
Thus, Option C is the correct option.