Question

Sigma notation -3(4)^n-1 n=2

Answer 1

`\bf \qquad \qquad \textit{sum of a finite geometric sequence}\\\\S_n=\sum\limits_(i=1)^(n)\ a_1\cdot r^(i-1)\implies S_n=a_1\left( \cfrac{1-r^n}{1-r} \right)\quad \begin{cases}n=n^(th)\ term\\a_1=\textit{first term's value}\\r=\textit{common ratio}\end{cases}\\\\\\~~~~~~~~~~~~~~~~~~\sum\limits_(n=2)^(5)~-3(\stackrel{\stackrel{r}{\downarrow }}{4})^(n-1)`

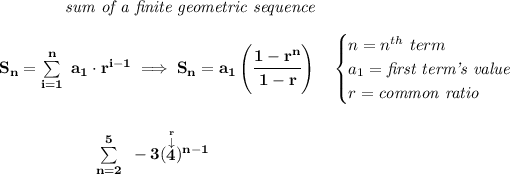
now, as you can see there, the common ratio is 4.

is it divergent or convergent?

well, the tale-tell fellow is the common ratio, if the common ratio is a fraction, is convergent, in this case it isn't, is 4, so is divergent.

a geometric serie is convergent only if the common ratio is a fraction, namely

0 < | r | < 1, is a value between 0 and 1.