Answer:

Explanation:
We have been given that triangle ABE is similar to triangle ACD. We rae asked to find the value of x.
We will use proportions to solve for x as similarity states that corresponding sides of two similar figures are proportional.
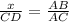
Upon substituting our given values in above proportion, we will get:
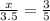
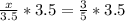
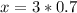

Therefore, the value of x is 2.1.