Question

On a particular day, the wind added 4 miles per hour to Alfonso's rate when he was cycling with the wind and subtracted 4 miles per hour from his rate on his return trip. Alfonso found that in the same amount of time he could cycle 57 miles with the wind, he could go only 33 miles against the wind. What is his normal bicycling speed with no wind?

Answer 1

Let Alfonso's normal bicycling speed with no wind be designates
`S`.

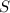Since the Time is common to both the cases of "with the wind" and "against the wind", let it be designated as
`T`.

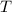Now, we know that "with the wind" Alfonso travels 57 miles in time, T and "against the wind" he travels 33 miles in the same time.

Also, since the speed of the wind is a constant 4miles per hour, we know that "with the wind" Alfonso's actual speed will be
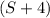`(S+4)` miles per hour and "against the wind" his speed will be
`(S-4)` miles per hour.

With all the information that is required let us proceed with the solution to the question. This will involve a formula which connects, actual speed, distance travelled and time taken to travel that distance. That formula is:

Distance=Actual Speed x Time Taken

Thus, in our question, the above equation for the two cases will be as:

For "with the wind"

`(S+4)* T=57`

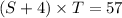
For "against the wind"

`(S-4)* T=33`

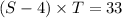
Now, expressing
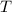`T`, in both the equations, in terms of the other parameters, we get:

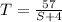`T=(57)/(S+4)` (from the "with the wind" condition) and

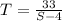`T=(33)/(S-4)` (from the "against the wind" condition)

Since
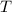`T` is the same in both the cases, we may equate the two equations to get:

`(57)/(S+4)=(33)/(S-4)`

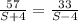
which after basic simplification yields:

`11S+44=19S-76`

`8S=120`

`\therefore S=15`

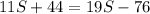
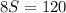
Thus, Alfonso's normal bicycling speed with no wind is 15 miles per hour.