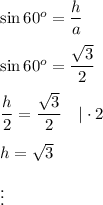Question

A regular hexagon has sides of 2 feet. What is the area of the hexagon?

Answer 1

Look at the picture.

The longer diagonals of the hexagon divide it into 6 equilateral triangles.

Method 1.

Use the Pythagorean theorem to calculate the height of triangle:

`a=2;\ (a)/(2)=(2)/(2)=1;\ h=?\\\\h^2+\left((a)/(2)\right)^2=a^2\\\\h^2+1^2=2^2\\h^2+1=4\ \ \ |-1\\h^2=3\to h=\sqrt3`

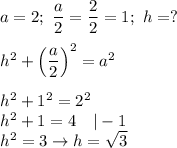
Calculate the area of the triangle:

`A_\triangle=(1)/(2)\cdot2\cdot\sqrt3=\sqrt3\ ft^2`

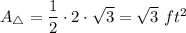
Calculate the area of the hexagon:

`A=6A_\triangle\to A=6\cdot\sqrt3=6\sqrt3\ ft^2`

Method 2:

Use the formula of the area of an equilateral triangle:

`A_\triangle=(a^2\sqrt3)/(4)\to A_\triangle=(2^2\sqrt3)/(4)=\sqrt3\ ft^2`

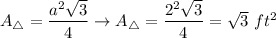
Calculate the area of the hexagon:

`A=6A_\triangle\to A=6\cdot\sqrt3=6\sqrt3\ ft^2`

Method 3.

Use the trigonometric function to calculate the height of a triangle:

`\sin60^o=(h)/(a)\\\\\sin60^o=(\sqrt3)/(2)\\\\(h)/(2)=(\sqrt3)/(2)\ \ \ |\cdot2\\\\h=\sqrt3\\\\\vdots`

Answer 2

Trigonometry would help with this question.

The area of a regular hexagon is ((3√3)s^2)/2 where s is the side.

Plugging in 2 gives us 6√3 or 10.39 feet.