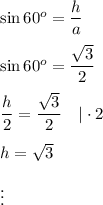Look at the picture.
The longer diagonals of the hexagon divide it into 6 equilateral triangles.
Method 1.
Use the Pythagorean theorem to calculate the height of triangle:
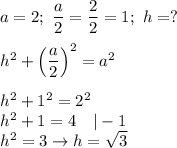
Calculate the area of the triangle:
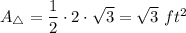
Calculate the area of the hexagon:
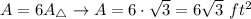
Method 2:
Use the formula of the area of an equilateral triangle:
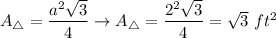
Calculate the area of the hexagon:
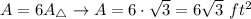
Method 3.
Use the trigonometric function to calculate the height of a triangle: