Question

The number of accidents on a particular highway average 4.4 per year.

a. identify the probability distribution of random variable x – number of accidents on a particular highway per year. (name and parameters)
b. what is the probability that there are exactly four accidents next year?
c. what is the probability that there are more than three accidents next year?

Answer 1

It is given that number of accidents on a particular highway is average 4.4 per year.

a. Let X be the number of accidents on a particular highway.

X follows Poisson distribution with mean μ =4.4

The probability function of X , Poisson distribution is given by;

P(X=k) =
`(e^(-4.4) (4.4)^(k))/(k!)`

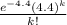
b. Probability that there are exactly four accidents next year, X=4

P(X=4) =
`(e^(-4.4) (4.4)^(4))/(4!)`

P(X=4) = 0.1917

Probability that there are exactly four accidents next year is 0.1917

c. Probability that there are more that three accidents next year is

P(X > 3) = 1 - P(X ≤ 3)

= 1 - [ P(X=3) + P(X=2) + P(X=1) + P(X=0)]

P(X=3) =
`(e^(-4.4) (4.4)^(3))/(3!)`

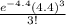
P(X=3) = 0.1743

P(X=2) =
`(e^(-4.4) (4.4)^(2))/(2!)`

P(X=2) = 0.1188

P(X=1) =
`(e^(-4.4) (4.4)^(1))/(1!)`

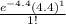
P(X=1) = 0.054

P(X=0) =
`(e^(-4.4) (4.4)^(0))/(0!)`

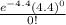
= 0.0122

Using these probabilities into above equation

P(X > 3) = 1 - P(X ≤ 3) = 1 - [ P(X=3) + P(X=2) + P(X=1) + P(X=0)]

= 1 - (0.1743 + 0.1188 + 0.054 + 0.0122)

P(X > 3) = 1 - 0.3593

P(X > 3) = 0.6407

Probability that there are more than three accidents next year is 0.6407