Question

Find the measure of Angle T.

Answer 1

Draw the center O, then TRO and TSO are right angles, adding to 180 degrees. As a quadrilateral's angles add to 360 degrees, ROS and T are supplementary. Sinec ROS=103 degrees, T=77 degrees.

Answer: 77°

Answer 2

`m\angle T=77^(\circ)`

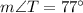
Explanation:

We have been given a diagram. We are asked to find the measure of angle T.

We can see that angle T is formed by two tangents from the same point.

We know that measure of angle formed by two intersecting tangents is half the difference of corresponding arcs.

First of all we will find measure of arc RQS as:

`\widehat{RQS}=360^(\circ)-103^(\circ)`

`\widehat{RQS}=257^(\circ)`

`m\angle T=\frac{\widehat{RQS}-\widehat{RS}}{2}`

`m\angle T=(257^(\circ)-103^(\circ))/(2)`

`m\angle T=(154^(\circ))/(2)`

`m\angle T=77^(\circ)`

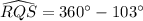
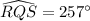
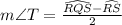
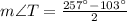
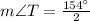
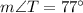
Therefore, the measure of angle T is 77 degrees.