Looks more like Trig than Algebra II
They want us to apply the sum angle formula to
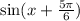
5π/6 is 150°; I find it easier to think in degrees.
When the tangent of x is 3/4 that's a right triangle with opposite 3, adjacent 4 so hypotenuse 5. So a sine of 3/5 and a cosine of 4/5, both positive because we're told x is in the first quadrant.
The sine sum angle formula is
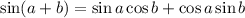
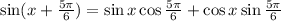
We know sin 150° = sin 30° = 1/2 and cos 150° = - cos 30° = -√3/2
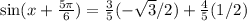
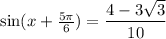
Third choice