Answer:
Option B. 2.2 miles.
Explanation:
A pilot of a small plane must begin a 10° descent starting from a height of 1983 feet above the ground that is AB is the height of plane above the ground, AB= 1983 feet. and A is the point from where the pilot starts descent.
thus, ∠ACB = ∠DAC = 10°
We have to find the distance between the runway and the airplane where it start this approach that is we have to find length AC( in miles).
Let AC = x
Applying trigonometric ratio,
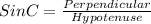
Put the values into the formula
sin 10° =
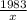
0.1737 =
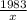
x =

x= 11419.64
The distance from the runway to the airplane is 11419.64 feet.
As we know 1 mile = 5280 feet
11419.64 feet =
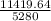
= 2.16 miles ≈ 2.2 miles
Option B. 2.2 mi is the correct answer.