Question

Complete the square to rewrite y=x^2 - 6x + 16 in vertex form

Answer 1

So remember that vertex form is
`y=a(x-h)^2+k`

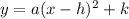
Firstly, put x^2 - 6x into parentheses:
`y=(x^2-6x)+16`

Next, to make what's inside the parentheses a perfect square, we need to divide the x coefficient by 2 and square that result. In this case: -6/2 = -3; (-3)^2 = 9. Add 9 into the parentheses, and subtract 9 on the outside of the parentheses:
`y=(x^2-6x+9)+16-9`

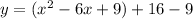
Next, factor (x^2-6x+9) to (x - 3)^2 and combine like terms outside of the parentheses, and your answer should be:
`y=(x-3)^2+7`

Answer 2

y= x² - 6x + 16

To complete the square we are going to use formula (a-b)² = a²- 2ab +b²

y= x² - 6x + 16 = x² -2*3x +3² -3² +16 = (x-3)² -9+16 = (x-3)² + 7

So,

y= (x-3)² + 7, vertex form pf the parabola y=x² - 6x + 16.

Vertex (3, 7).