Question

If triangleabc and trianglepqr are similar​ triangles, find qr and pr.

Answer 1

we have two similar triangles.

we know that in similar traingles ratios of the corresponding sides are always equal.

we have AB is propotional to PQ

BC is propotional to QR

AC is propotionbal to PR

here we dont have the lengths of sides

`image`

so the length of PR and QR will be equal to some constant have same value .

Answer 2

Answer: PR = 20; QR = 25

Step-by-step explanation: Similar triangles means the triangles have their sides proportional to one another.

In the picture from attachment, Triangle ABC has sides:

AB = 9

BC = 15

AC = 12

Triangle PQR is proportional to ABC, which means:

AB is proportional to PQ

AC is proportional to PR

Bc is proportional to QR

Or,

`(PQ)/(AB) = (PR)/(AC) = (QR)/(BC)`

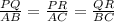
PQ, AB and AC is known, so calculate PR:

`(15)/(9)=(PR)/(12)`

PR =
`(15.12)/(9)`

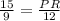
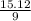
PR = 20

With PR, find QR:

`(15)/(9) = (QR)/(15)`

QR =
`(15.15)/(9)`

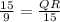
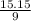
QR = 25

QR measures 25 and PR measures 20