No, we do not multiply the first equation by 2 and then add it to the second equation. We have to multiply the first equation by 4.
To illustrate this point, consider system A:
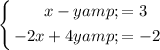
If we multiply the first equation by 2, we get
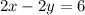
Now, if we replace the second equation with the sum of the second equation and
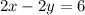 , we get
, we get
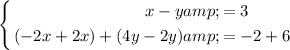
which simplifies to

This is not an equivalent system to System B. We can see that we ended up with a 2y = 4 equation.
In order to end up with a 2x = 10 second equation, we have to multiply the first equation of system A by 4 to get
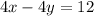
If we replace the second equation with the sum of the second equation and
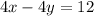 , we get
, we get

which simplifies to
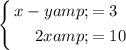
Otherwise, you are correct. The solution to system B is the solution to system A. Adding an equation to another does not change the system.