The two possible values of
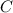 is option
is option
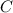
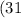 and
and
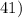 .
.
Given,
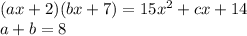
Simplify the equation of LHS as,
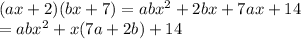
Compare LHS and RHS as,
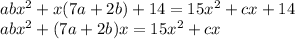
The two equations are:
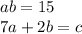
From the given,
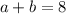
Subtract
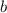 on both sides in the equation as,
on both sides in the equation as,
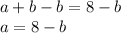
Substitute
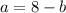 in the equation
in the equation
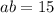 as,
as,
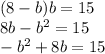
Solve the equation by setting equal to zero as,
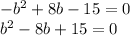
Factorize the equation as follows:
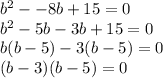
Solve the factors as,
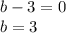
And
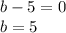
Substitute
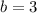 in
in
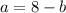 as,
as,
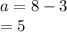
Thus,
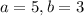 .
.
Substitute
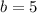 in
in
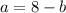 as,
as,
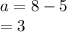
Thus,
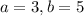 .
.
Substitute
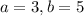 in the equation
in the equation
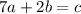 as,
as,
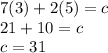
Substitute
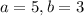 in the equation
in the equation
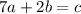 as,
as,
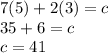
Thus, the two possible values of
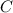 is
is
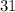 and
and
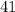 .
.