Question

In a polynomial equation, the sum of the multiplicities of the roots always add up to.. the degree of the polynomial. the leading coefficient of the polynomial. the constant coefficient of the polynomial the sum of the coefficients of the polynomial.

Answer 1

the degree of the polynomial

Explanation:

Given

Polynomial equation

Required

What does the sum of the multiplicities add up to

To answer this question, I'll make use of the following polynomial.

`p(x) = x^3 - 7x^2 + 15x - 9`

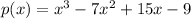
When factorized, the polynomial is:

`p(x) = (x - 1)(x - 3)(x-3)`

`p(x) = (x - 1)(x - 3)^2`

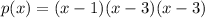
x-1 can be expressed as
`(x - 1)^1`

So, we have:

`p(x) = (x - 1)^1(x - 3)^2`

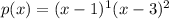
The sum of multiplicity (M) of the equation is 3.

This is so because

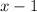`x - 1` occurred one time in
`p(x) = (x - 1)(x - 3)^2`

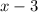`x - 3` occurred two times in
`p(x) = (x - 1)(x - 3)^2`

`Sum= 1 + 2`

`Sum= 3`

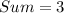
The degree of
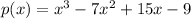`p(x) = x^3 - 7x^2 + 15x - 9` or
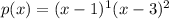`p(x) = (x - 1)^1(x - 3)^2` is 3.

This implies that:

`Sum = Degree = 3`

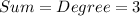
Hence: Option (a) answers the question