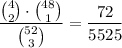We're drawing 3 cards from a deck of 52, and we have
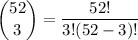
ways of drawing any 3-card hand.
Of the 4 total aces in the deck, we want to draw 2. The third card can be any 1 of the 48 remaining cards. We have
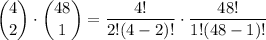
possible 3-card hands that contain any 2 aces.
The probability of drawing such a hand is then