The question is incomplete. Here is the complete question.
USA Today reported that 36% of adult drivers admit that they often or sometimes talk on a cell phone when driving. This was based on a random sample of 1004 adult drivers.
a) What is a 90% confidence interval for the true proportion of adult drivers who have often or sometimes talk on a cell phone when driving?
b) What is a 95% confidence interval for the true proportion of adult drivers who have often or sometimes talk on a cell phone when driving?
c) What is a 99% confidence interval for the true proportion of adult drivers who have often or sometimes talk on a cell phone when driving?
d) What do you notice?
Answer and Step-by-step explanation: The way to calculate confidence interval for proportions is by using the following formula:

where
p is the sample population proportion
n is the number of individuals in the sample
z is z-score associated of the % of confidence
a) A 90% confidence has a z-score of z = 1.645
Calculating:
Interval =
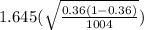
Interval =
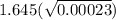
Interval =

Interval = 0.025
A 90% Confidence interval for true population is between 0.335 and 0.385.
b) A 95% confidence has a z-score of z = 1.96
Since the sample parameter didn't change, the interval will be:
Interval = 1.96(0.01515)
Interval = 0.03
For a 95% confidence, interval is between 0.33 and 0.39.
c) A 99% confidence has a z-score of z = 2.58
Interval = 2.58(0.01515)
Interval = 0.39
For a 99% confidence, interval is between -0.03 and 0.75
d) Confidence interval tells you how certain your results from polling or survey would represent the real population's behaviour. In the experiment above, as the percentage of certainty grows, closer the real population proportion actually is for adult drivers who often or sometimes talk on a cell phone when driving.