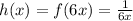Answer:
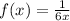
Explanation:
If a transformed function of f(x) is,
f(x) = a f[b(x-h)] + k
Then, b represents the horizontal compression ( When b > 1 ) or stretch ( when 0 < b < 1 )
Here, the given function is,
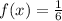
Thus, the transformed function obtained by compressing f(x) by the scale factor of 6 is,