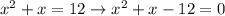Question

What are the values of a, b, and c in the quadratic formula given the equation 3x^2-x= 4?

a. a=3, b=0, c=-4B. a=3, b=1, c=4C. a=3, b=1, c=4D. a=3, b=-1, c=-42. What is the first correct step for solving the equation, x^2+x=12 ?

Answer 1

First question:

First of all, you have to rewrite the quadratic equation bringing everything to the left hand side, so you have

`3x^2 - x = 4 \iff 3x^2 - x - 4 = 0`

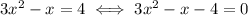
Now, the coefficients of a quadratic equation are usually read as
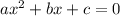`ax^2 + bx + c = 0`, i.e.
`a` is the coefficient of
`x^2`,
`b` is the coefficient of
`x` and
`c` is the constant term.

Once you rewrite your equation, the coefficient of
`x^2` is 3, the coefficient of
`x` is
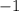`-1` and the constant term is
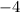`-4`, so the correct answer is D.

Second question:

As discussed above, the first step for solving a quadratic equation is bringing everything to the left, so that you are in the form
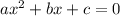`ax^2 + bx + c = 0`. So, the first thing you have to do is to transform

`x^2+x=12 \to x^2 + x - 12 = 0`