Question

What are potential solutions to 2ln(x+3)=0

Answer 1

When solving logarithmic/natural log equations, the strategy is to get ln (x) alone on one side, and all the stuff on the other side. Then exponentiate both sides to get to x.

2 ln (x + 3) = 0

ln (x + 3) = 0

At this point, we can't isolate anymore or use logarithm properties to separate this further. But we have ln (something), and we can exponentiate.

`e^(ln(x+3)) = e^(0)`

`e^(ln(x+3)) = 1`

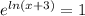
x+3 = 1 <--This come from the fact the ln (x) and
`e^(x)` are inverse functions that undo each other. This is why exponentiating works.

x = -2

So x = -2 is our solution.

Answer 2

B. x= -2 and x= -4

Explanation:

edge 2021