Question

A math teacher claimed that the average grade of the students in her Algebra 2 classes this year would be equal to the average grade of the same students in Algebra 1 classes last year. The average grade of last year’s Algebra 1 students was an 87%. In a random sample of 30 current Algebra 2 students, the average grade was 86%, with a standard deviation of 3%. Is there enough evidence to reject the teacher's claim?

Enter your answer as a z-value and either yes or no, separated by a comma, like this: -4.25, yes

Answer 1

These questions should be asked more clearly.

If 3% is the standard deviation of the average then a 1% decrease in score is a z=-1/3, which is small in absolute value, so we can't reject the claim. In this interpretation we'd answer: -0.33, no.

But if we'll assume 3% is the standard deviation of the individual samples, it's a different story. We use percent as our unit. The standard deviation of the average is

`3/√(30)=0.55`.

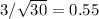So we get a z (really a t) here of

`z = (86 - 87)/(0.55) = -1.8`

That's kinda borderline, a one sided t test with 29 dfs will give about the same probability as the normal distribution for a tail z=1.8, p=.036 aka p=3.6%. Typically we'd choose a 1% or 5% rejection threshold before we started; this one is in between.