It depends on the value of b
Exponential functions are defined for positive values of the base [ŧex] b [/tex]. Also, they're not defined if
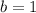 , or at least let's say that this is a trivial case, since it is the constant function 1.
, or at least let's say that this is a trivial case, since it is the constant function 1.
Case 0<b<1:
If the base sits between 0 and 1, the exponential function is constantly decreasing. The explanation is quite intuitive, assume for the sake of simpleness that b is rational. If it sits between 0 and 1, it means that it can be written as a fraction p/q, with p<q. So, if you give a large exponent to b, you obtain
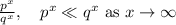
On the other hand, if you consider negative exponents, you switch numerator and denominator and then raise to the same exponent the fraction q/p, which gets larger and larger.
So, if 0<b<1, we have
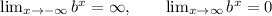
and thus 0 is a horizontal asymptote as x tends to (positive) infinity.
Case b>1:
This case is very similar, except all roles are inverted. Now you start with a fraction p/q where p>q. So, with positive, large exponents you get
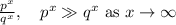
And as before, negative exponents switch numerator and denominator, so the fraction becomes q/p and thus you have

So, again, 0 is a horizontal asymptote, but this time for x tending towards negative infinite.