Question

What best describes the asymptote of an exponential function of the form f(x)=b^x?

Answer 1

It depends on the value of b

Exponential functions are defined for positive values of the base [ŧex] b [/tex]. Also, they're not defined if
`b=1`, or at least let's say that this is a trivial case, since it is the constant function 1.

Case 0<b<1:

If the base sits between 0 and 1, the exponential function is constantly decreasing. The explanation is quite intuitive, assume for the sake of simpleness that b is rational. If it sits between 0 and 1, it means that it can be written as a fraction p/q, with p<q. So, if you give a large exponent to b, you obtain

`(p^x)/(q^x),\quad p^x \ll q^x \text{ as } x \to \infty`

On the other hand, if you consider negative exponents, you switch numerator and denominator and then raise to the same exponent the fraction q/p, which gets larger and larger.

So, if 0<b<1, we have

`\lim_(x \to -\infty) b^x = \infty,\qquad \lim_(x \to \infty) b^x = 0`

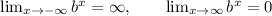
and thus 0 is a horizontal asymptote as x tends to (positive) infinity.

Case b>1:

This case is very similar, except all roles are inverted. Now you start with a fraction p/q where p>q. So, with positive, large exponents you get

`(p^x)/(q^x),\quad p^x \gg q^x \text{ as } x \to \infty`

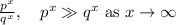
And as before, negative exponents switch numerator and denominator, so the fraction becomes q/p and thus you have

`\lim_(x \to -\infty) b^x = 0,\qquad \lim_(x \to \infty) b^x = \infty`

So, again, 0 is a horizontal asymptote, but this time for x tending towards negative infinite.

Answer 2

Horizontal asymptote at y=0