Answer:
The probability of flipping a coin 8 times and getting heads 3 times is 21.9%
Explanation:
Given
A coin
A coin has two sides (a head and a tail)
The probability of getting a head is equal to the probability of getting a tail;
Let these probabilities be represented by H and P;
i.e. H = Probability of getting a Head
T = Probability of getting a Tail
Since both probabilities are equal and probability always sum to 1 then
H + T = 1
H + H = 1
2H = 1
H = 0.5 and T = 0.5
P (3 heads in 8 tosses) is given by the binomial representation
![\left[\begin{array}{c}&n\\&r\end{array}\right] * H^(r) * T^(n - r)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/kz1rfn8193w6vh0uqs4num1ziehek0s6bo.png)
Where n = number of tosses = 8
r = number of heads
By Substitution,
![\left[\begin{array}{c}&n\\&r\end{array}\right] * H^(r) * T^(n - r)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/kz1rfn8193w6vh0uqs4num1ziehek0s6bo.png) becomes
becomes
![\left[\begin{array}{c}&8\\&3\end{array}\right] * 0.5^(3) * 0.5^(8 - 3)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/dt2tfbtpy9c4m4qp52o8as1zyfyho5bx1q.png)
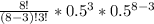
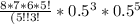
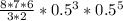
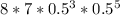
= 0,21875
= 21.875%
= 21.9% --- Approximately