Question

A sample poll of 100 voters chosen at random from all voters in a given district indicated that 55 of them were in favor of a particular candidate. find the 99% confidence limits for the proportion of all voters in favor of this candidate.

Answer 1

The
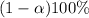`(1-\alpha )100\%` confidence interval for proportion is

`p \pm z_(\alpha /2) \sqrt{(p(1-p))/(n)}`

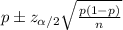
Here
`p=(55)/(100)=0.55,\alpha =0.01`

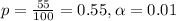
Using standard normal tables
`z_(\alpha /2)=-2.576`.

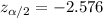The 99% confidence interval for proportion is

`0.55 \pm 2.576\sqrt{(0.55(1-0.55))/(100)}`

`(0.422,0.678)`

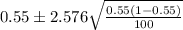
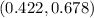
The CI interpretation is that "We are 99% confident that the proportion of voters in favor of the candidate lies between 0.422 and 0.678".