The
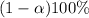 confidence interval for proportion is
confidence interval for proportion is
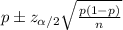
Here
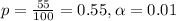
Using standard normal tables
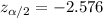 .
.
The 99% confidence interval for proportion is
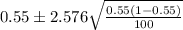
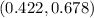
The CI interpretation is that "We are 99% confident that the proportion of voters in favor of the candidate lies between 0.422 and 0.678".