Our strategy will aim to factor the polynomial as much as possible: once completely factored, the polynomial will become a multiplication of polynomials of lower degree:
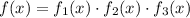
and its zeroes will be the ones of its factors.
Since the polynomial has no constant term, you can factor it as follows:
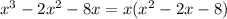
To continue, we must factor the quadratic expression in the parenthesis. A common way to factor expressions like
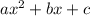 is to find the two solutions
is to find the two solutions
 and
and
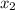 and write the polynomial as
and write the polynomial as
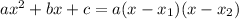 .
.
To find the solutions, we can use the quadratic formula
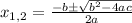
and since in our case
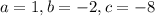 , the solving formula becomes
, the solving formula becomes
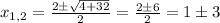
So, the two solutions are
 and
and
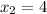 and we write the polynomial as
and we write the polynomial as
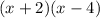 .
.
So, the complete factorization is
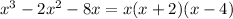
So, the zeroes of the cubic polynomial we started with are the zeroes of the three polynomials in the factorization:
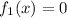 yields a solution for
yields a solution for
 ,
,
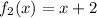 yields a solution for
yields a solution for
 and
and
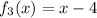 yields a solution for
yields a solution for
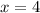 .
.