Question

Solve: 2|x + 7|−4 ≥ 0

Express the answer in set-builder notation.


A. x

B. x

C. x

D. -9 < x < -5

Answer 1

The first one is C) x<= -9 or x=> -5

The second one is (-infinity, -9] U [-5, infinity)

I just did it

Answer 2

To solve an absolute inequality first step is to isolate absolute value expression.

Hence remove -4 from the left side. So, add 4 to each sides of the inequality.

2|x + 7|−4 ≥ 0

2|x + 7|−4 +4≥ 0 +4

2|x + 7| ≥ 4 Combine the like terms.

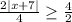`(2|x+7|)/(4) \geq (4)/(2)` Divide each sides by 2.

|x + 7| ≥2

Next step is to remove the absolute value sign. So,

x + 7≥2 and x+7≤-2.

x≥2-7 and x≤-2-7

x≥-5 and x≤-9

So, the correct choice is C. x ≤ -9 or x ≥ -5.