Speed is the ratio of distance and time.
So, average speed= Total distance/ total time.
Let's assume t is the time taken for going from New Orleans to Boston and it's taking 1 hour less to return back. So, time taken for return back is t-1.
Given the speed from New Orleans to Boston is 40 mph. So,
Distance = Speed * time
So, d =40 t
Hence t= d/40
Similarly Distance for returning back:
d =80 (t-1)
d/80 = t-1 (Dividing 80 to each sides)
Now the total distance= d+ d = 2d
And total time : t + t -1= d/40 + d/80
So, the average speed =
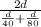
=
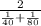 (cancel out d )
(cancel out d )
Common denominator of 40 and 80 is 80. So, multiply each terms by 80.
=
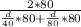
=
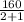
=
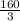
=53.33 mph
So, the average speed is 53.33 mph.