Question

A train goes from New Orleans to Boston at 40 mph. On the way back it returns with a speed 80 mph. If it takes it an hour less time to return, what is its average speed?

Answer 1

Speed is the ratio of distance and time.

So, average speed= Total distance/ total time.

Let's assume t is the time taken for going from New Orleans to Boston and it's taking 1 hour less to return back. So, time taken for return back is t-1.

Given the speed from New Orleans to Boston is 40 mph. So,

Distance = Speed * time

So, d =40 t

Hence t= d/40

Similarly Distance for returning back:

d =80 (t-1)

d/80 = t-1 (Dividing 80 to each sides)

Now the total distance= d+ d = 2d

And total time : t + t -1= d/40 + d/80

So, the average speed =
`(2d)/((d)/(40)+(d)/(80))`

=
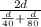
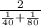`(2)/((1)/(40)+(1)/(80))` (cancel out d )

Common denominator of 40 and 80 is 80. So, multiply each terms by 80.

=
`(2*80)/((d)/(40)*80+(d)/(80)*80)`

=
`(160)/(2+1)`

=
`(160)/(3)`

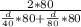
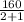
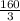
=53.33 mph

So, the average speed is 53.33 mph.