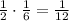Question

A box contains 6 identically sized, solid-colored balls. one ball is green, 2 are yellow, and 3 are red. a ball is drawn at random and returned to the box, then a second ball is drawn at random. what is the probability that the first ball is red and the second ball is green?

Answer 1

When you draw the first ball, you have three positive outcomes (the three red balls) and 6 possible outcomes (any of the six balls in the box).

This means that the probabilty of getting a red ball in the first draw is

`(3)/(6) = (1)/(2)`

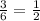
since you return the first drawn ball to the box, the second drawn takes place with the same conditions as the first, exept this time you're looking for a green ball, and thus you only have one positive outcome. So, the probability of getting a green ball is

`(1)/(6)`

The probability of two independent events occuring one after the other is the product of the two probabilities, so the answer to your question is

`(1)/(2)\cdot(1)/(6) = (1)/(12)`