(cos x - (sqrt 2)/2)(sec x -1)=0 I. Use the zero product property to set up two equations that will lead to solutions to the original equation. II. Use a reciprocal identity to express the equation involving - QAmmunity.org

(cos x - (sqrt 2)/2)(sec x -1)=0 I. Use the zero product property to set up two equations that will lead to solutions to the original equation. II. Use a reciprocal identity to express the equation involving

asked Nov 11, 2019 126k views

2 Answers

Answer and explanation :

Given :
$(\cos x-(√(2))/(2))(\sec x-1)=0$

To find :

I. Use the zero product property to set up two equations that will lead to solutions to the original equation.

Solution :

The zero product property state that,

If
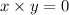x* y=0 then x=0 or y=0 (or both x=0 and y=0)

Applying zero product property we get,

$(\cos x-(√(2))/(2))(\sec x-1)=0$

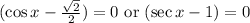
$(\cos x-(√(2))/(2))=0\text{ or }(\sec x-1)=0$

The two equations form is

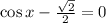$\cos x-(√(2))/(2)=0$ ....(1)

$\sec x-1=0$ ......(2)

II. Use a reciprocal identity to express the equation involving secant in terms of sine, cosine, or tangent.

Solution :

The reciprocal identity is flipping of a number,

The reciprocal of secant is 1 by cosine

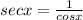
sec x=(1)/(cos x)

Substitute in the given equation,

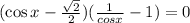
$(\cos x-(√(2))/(2))((1)/(cos x)-1)=0$

III. Solve each of the two equations in Part I for x, giving all solutions to the equation

Solution :

The two equations form is

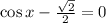$\cos x-(√(2))/(2)=0$ ....(1)

$\sec x-1=0$ ......(2)

Solving equation (1)

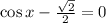
$\cos x-(√(2))/(2)=0$

$\cos x-{1}\frac{√(2)}=0$

$\cos x={1}\frac{√(2)}$

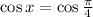
$\cos x=\cos (\pi)/(4)$

$x=(\pi)/(4)$

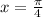
Solving equation (2)

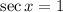
$\sec x-1=0$

$\sec x=1$

$\sec x=\sec 0$

x=0

Therefore, The solutions of the equation is
$x=0,(\pi)/(4)$

Zona answered Nov 16, 2019

by Zona

5.0k points

Search QAmmunity.org