When we get a question with "probability of at least two the same" we should think of it as 1 minus the probability of all different.
Rather than dazzle you with chooses and factorials let's work our way up to it.
If there was only one lady, there's probability 1 no two will choose the same style.
With two ladies, the second has a 13/14 th chance of choosing a different coat.
With three ladies , the probability of all different is
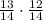
With eight ladies, we get seven fractions. We'll do 1 minus to get "two or more the same":
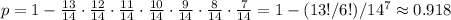
Second choice
5 boys 12 watch styles
P(Two boys different),=11/12
P(Three boys different),=11/12 * 10/12
P(Five boys different) = 11*10*9*8/12^4 = .3819
P(two of five match) = 1 - 11*10*9*8/12^4 = .6181
last choice