We assume the lunch prices we observe are drawn from a normal distribution with true mean
 and standard deviation 0.68 in dollars.
and standard deviation 0.68 in dollars.
We average
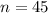 samples to get
samples to get
 .
.
The standard deviation of the average (an experiment where we collect 45 samples and average them) is the square root of n times smaller than than the standard deviation of the individual samples. We'll write
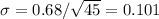
Our goal is to come up with a confidence interval (a,b) that we can be 90% sure contains
 .
.
Our interval takes the form of
 as
as
 is our best guess at the middle of the interval. We have to find the z that gives us 90% of the area of the bell in the "middle".
is our best guess at the middle of the interval. We have to find the z that gives us 90% of the area of the bell in the "middle".
Since we're given the standard deviation of the true distribution we don't need a t distribution or anything like that. n=45 is big enough (more than 30 or so) that we can substitute the normal distribution for the t distribution anyway.
Usually the questioner is nice enough to ask for a 95% confidence interval, which by the 68-95-99.7 rule is plus or minus two sigma. Here it's a bit less; we have to look it up.
With the right table or computer we find z that corresponds to a probability p=.90 the integral of the unit normal from -z to z. Unfortunately these tables come in various flavors and we have to convert the probability to suit. Sometimes that's a one sided probability from zero to z. That would be an area aka probability of 0.45 from 0 to z (the "body") or a probability of 0.05 from z to infinity (the "tail"). Often the table is the integral of the bell from -infinity to positive z, so we'd have to find p=0.95 in that table. We know that the answer would be z=2 if our original p had been 95% so we expect a number a bit less than 2, a smaller number of standard deviations to include a bit less of the probability.
We find z=1.65 in the typical table has p=.95 from -infinity to z. So our 90% confidence interval is
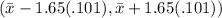
in other words a margin of error of
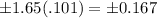 dollars
dollars
That's around plus or minus 17 cents.