Answer:
The correct option is A.
Explanation:
Given: ΔABC
Prove: Mid segment between sides AB and BC is parallel side AC.
Let the vertices of triangle are A(0,0), B(x₁,y₁) and C(x₂,0).
Midpoint Formula:
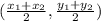
The midpoint of AB is
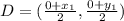 (Using the midpoint formula)
(Using the midpoint formula)
The midpoint of AB is
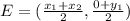 (Using the midpoint formula)
(Using the midpoint formula)
Slope Formula:
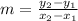
The slope of DE is
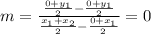
The slope of AC is
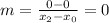
Slope of AC and DE are same, therefore the lines AC and DE are parallel because slope of two parallel lines are same.
The correct statement is "The coordinates of D and E were found using the midpoint formula".
Therefore the correct option is A.