Answer:
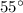
Step-by-step explanation:
Since, The angle subtended at the center of a circle is double the size of the angle subtended at the edge from the same two points,
Therefore,
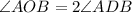
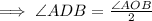
But,
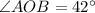
Therefore,
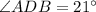
Similarly,
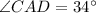 ( because, it is given that,
( because, it is given that,
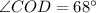 )
)
Since,
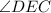 is the exterior angle of
is the exterior angle of
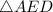
Thus,
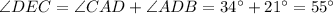
⇒
