At n=0 that looks like 2(6^0)-5(6^0)-2 = -5, a counterexample.
-----------------
It works for n=1 and n=2 so let's try to prove it for natural n>0.
I've been warned off using "mod" in answers so we'll kind of handwave around it.
We substitute n=m+1 so m is a non-negative integer, m >= 0.
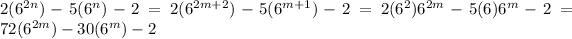
The term times 30 will always be a multiple of 10, so we need to check the rest of it is as well. The factor of 72=70+2 and the 70 part will always give a multiple of 10.
Also
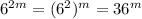 and that will have the same remainder as
and that will have the same remainder as
 when divided by 10. In fact every power of 6 except the zeroth ends in 6, because 6 times 6 is 36.
when divided by 10. In fact every power of 6 except the zeroth ends in 6, because 6 times 6 is 36.
So we must show
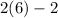
is a multiple of 10 which of course it is. We also need to check m=0, 2(1)-2=0, ok as well. That ends the proof.