Question

Prove that 2(6^2n)-5(6^n)-2 is divisible by 10 for all values of n.

Answer 1

At n=0 that looks like 2(6^0)-5(6^0)-2 = -5, a counterexample.

-----------------

It works for n=1 and n=2 so let's try to prove it for natural n>0.

I've been warned off using "mod" in answers so we'll kind of handwave around it.

We substitute n=m+1 so m is a non-negative integer, m >= 0.

`2(6^(2n))-5(6^n)-2= 2(6^(2m + 2)) - 5(6^(m+1)) -2 = 2(6^2)6^(2m) - 5(6)6^m - 2 = 72( 6^(2m) ) - 30 (6^m) - 2`


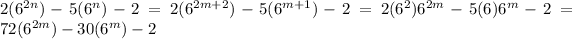
The term times 30 will always be a multiple of 10, so we need to check the rest of it is as well. The factor of 72=70+2 and the 70 part will always give a multiple of 10.


Also
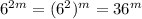`6^(2m)= (6^2)^m= 36^m` and that will have the same remainder as
`6^m` when divided by 10. In fact every power of 6 except the zeroth ends in 6, because 6 times 6 is 36.

So we must show


`2( 6)- 2`

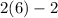
is a multiple of 10 which of course it is. We also need to check m=0, 2(1)-2=0, ok as well. That ends the proof.