Answer:
The magnitude of the coefficient of kinetic friction is approximately 1.304 × 10⁻⁵
Step-by-step explanation:
The given parameters are;
The time it takes for the box to stop, "t" = 600 seconds
The distance the box moves before coming to a stop, "d" = 23 meters
The work done by the friction force to stop the block = The kinetic energy lost by the box
The work done by the friction force to stop the block =
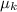 ·m·g·d
·m·g·d
The kinetic energy change of the block = 1/2·m·u²
Where;
g = The acceleration due to gravity = 9.8 m/s²
m = The mass of the box
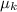 = The coefficient of kinetic friction
= The coefficient of kinetic friction
d = The distance travelled by the block = 600 m
u = The initial velocity of the block
∴
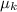 ·m·g·d = 1/2·m·u²
·m·g·d = 1/2·m·u²
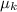 ·g·d = 1/2·u²
·g·d = 1/2·u²
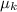 = 1/2·u²/(g·d) = 1/2·u²/(9.8 × 23) = u²/450.8
= 1/2·u²/(g·d) = 1/2·u²/(9.8 × 23) = u²/450.8
∴
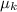 = u²/450.8...(1)
= u²/450.8...(1)
The kinematic equation of motion of the block can be presented as follows;
v = u - a·t
Where;
v = The final velocity = 0 m/s (The block slides to a stop)
u = The initial velocity
a = The acceleration of the block (the minus sign indicates that the block's velocity is decreasing)
t = The time of motion of the block = 600 seconds
Therefore, by substituting the above values, we have;
0 = u - 600·a
∴ u = a·600
The kinematic equation of motion for the distance moved by the block, "s" can be expressed as follows;
s = u·t - 1/2·a·t²
Where;
s = The distance moved by the bloc = 23 meters
∴ 23 = a·600·600 - 1/2·a·600² = 360,000·a - 1/2·a·360,000 = 180,000·a
a = 23/(180,000)
u = 600 × (23/(180,000)) = 23/300
The initial velocity, u = 23/300 m/s
From equation (1), we have;
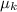 = u²/(450.8) = (23/300)²/450.8 = 23/1764000 ≈ 1.304 × 10⁻⁵
= u²/(450.8) = (23/300)²/450.8 = 23/1764000 ≈ 1.304 × 10⁻⁵
The magnitude of the coefficient of kinetic friction,
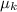 ≈ 1.304 × 10⁻⁵
≈ 1.304 × 10⁻⁵