Use tan x = 5/12 where 0 < x < 90, to answer the following questions. Part A: what is sin x? Part B: what is cos x? Part C: what is sin(x + 2pi/3)? Please help and thank y…

Question

asked Dec 5, 2019 31.2k views

1 Answer

Stux · Answer 1 · 2019-12-09T22:06:47+0000

Try this solution:

Part A: note, that tanx=1/ contanx. Using this property and formula 1+contan²x=1/ sin²x, it is possible to find sinx:

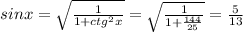
$sinx= \sqrt { (1)/(1+ctg^2x)}=\sqrt{(1)/(1+(144)/(25))}= (5)/(13)$

Part B: if tanx=5/12, then using the formula 1+tan²x=1/cos²x it is possible to find cosx:

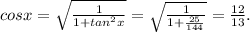
$cosx=\sqrt{(1)/(1+tan^2x)}=\sqrt{(1)/(1+(25)/(144))}=(12)/(13).$

Part C: note, that sin(x+2pi/3)=sinx*cos2pi/3+sin2pi/3*cosx=-0.5sinx+√3/2cosx, where sinx=5/13 and cosx=12/13.

$sin(x+(2 \pi)/(3))=(√(3))/(2) *(12)/(13)-(1)/(2) *(5)/(13)=(12√(3)-5)/(26)$