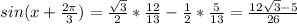Question

Use tan x = 5/12 where 0 < x < 90, to answer the following questions.

Part A: what is sin x?
Part B: what is cos x?
Part C: what is sin(x + 2pi/3)?

Please help and thank you. Btw the 0 and 90 are in degrees.

Answer 1

Try this solution:

Part A: note, that tanx=1/ contanx. Using this property and formula 1+contan²x=1/ sin²x, it is possible to find sinx:

`sinx= \sqrt { (1)/(1+ctg^2x)}=\sqrt{(1)/(1+(144)/(25))}= (5)/(13)`

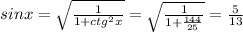
Part B: if tanx=5/12, then using the formula 1+tan²x=1/cos²x it is possible to find cosx:

`cosx=\sqrt{(1)/(1+tan^2x)}=\sqrt{(1)/(1+(25)/(144))}=(12)/(13).`

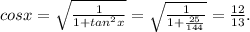
Part C: note, that sin(x+2pi/3)=sinx*cos2pi/3+sin2pi/3*cosx=-0.5sinx+√3/2cosx, where sinx=5/13 and cosx=12/13.

`sin(x+(2 \pi)/(3))=(√(3))/(2) *(12)/(13)-(1)/(2) *(5)/(13)=(12√(3)-5)/(26)`