Question

There are 100 cats in a population that follows hardy-weinberg conditions. 4 cats display a recessive white coat color. how many of the cats are heterozygous?

Answer 1

We know that Hardy-Weinberg conditions include the following equations:

`p^(2)+2pq+ q^(2)=1`

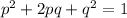
where
`p+q=1`

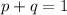
And where p = dominant, and q = recessive; this means that
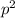`p^(2)` is equal to the homozygous dominant,
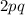`2pq` is the heterozygous, and
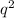`q^(2)` is the homozygous recessive .

So we have 100 total cats, with 4 having the recessive white coat color. That means we have a ratio of
`(4)/(100)` or 0.04. Let that equal our
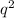`q^(2)` value.

So when we solve for q, we get:

`q^(2)=0.04`

`q=√(0.04) =0.2`

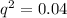
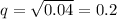
Now that we have our q value, we can use the other equation to find p:

`p+q=1`

`p+0.2=1`

`p=0.8`

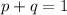
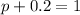
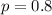
So then we can solve for our heterozygous population:

`2pq=2(0.8)(0.2)=0.32`

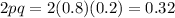
This is the ratio of the population. So we then multiply this number by 100 to get the number of cats that are heterozygous:

`0.32*100=32cats`

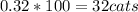
So now we know that there are 32 heterozygous cats in the population.