Question

The polynomial function f(x) is a fourth degree polynomial. Which of the following could be the complete list of the roots of f(x)?

A) 3, 4, 5, 6
B) 3, 4, 5, 6i
C) 3, 4, 4+sqrt6i, 5+sqrt6
D) 3, 4, 5 + i, –5 + i

Answer 1

the answer is A

Explanation:

Answer 2

Option A.

Explanation:

The polynomial function f(x) is a fourth degree polynomial.

According to complex conjugate root theorem, if a complex number (a+ib) is a root of a polynomial hen its conjugate (a-ib) is also a root of that polynomial.

In option A, all roots are real numbers, so it can be the list of all zeros of the fourth degree polynomial.

In option B, 6i is a root of f(x). By complex conjugate root theorem -6i is also a root of f(x), which is not given. So, option B is incorrect.

In option C,
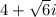`4+√(6)i` is a root of f(x). By complex conjugate root theorem
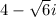`4-√(6)i` is also a root of f(x), which is not given. So, option C is incorrect.

In option D,
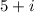`5+i` is a root of f(x). By complex conjugate root theorem
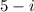`5-i` is also a root of f(x), which is not given. So, option D is incorrect.

Therefore, the correct option is A.