Question

Details: Cargo ship can carry 21,600 tons Cars weigh 3.6 tons each Trucks weigh 7.5 tons each y = number of cars x= number of trucks Your equation was 3.6y + 7.5x = 21600 Find the number of trucks that can be shipped if there are no cars.​

Answer 1

Given:

The equation is

`3.6y+7.5x=21600`

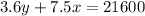
where, y is the number of cars and x is the number of trucks shipped.

To find:

The number of trucks that can be shipped if there are no cars.​

Solution:

We have,

`3.6y+7.5x=21600`

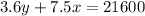
If there are no cars in the cargo ship, then y = 0 because y is the number of cars.

Putting y=0 in the given equation, we get

`3.6(0)+7.5x=21600`

`0+7.5x=21600`

`7.5x=21600`

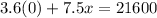
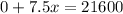
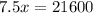
Divide both sides by 7.5.

`x=(21600)/(7.5)`

`x=2880`

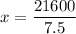
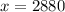
x is the number of trucks shipped.

Therefore, the number of trucks that can be shipped if there are no cars is 2880.