Answer: (-2,-2)
Explanation:
The parent function of the absolute function is f(x)=|x|.
General form of absolute function :
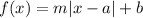 , where (a,b) is the vertex of the function.
, where (a,b) is the vertex of the function.
Also , when m<0 then the graph opens downwards.
when m>0 then the graph opens upwards.
Given : The absolute value function:
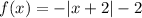
Comparing the given absolute function to with the general form of the absolute function , then we get
m= -1<0 , a= -2 and b= -2
Since m is negative , it means the graph of the function opens downwards .
∴, the vertex of the function is : (-2,-2)